図形問題と聞くと、「苦手だな…」「計算が面倒くさそう…」と感じる方もいらっしゃるかもしれません。しかし、今回ご紹介するのは、そんなイメージを覆す、まるでパズルのように解けるジュニア算数オリンピックの面白い問題です。この問題を解き終えたとき、あなたはきっと「算数って、こんなに面白いんだ!」と感動すること間違いなしです。小学生でも解けるように、平方根(ルート)を使わないという制約が、逆に思考の柔軟性を引き出してくれます。さあ、あなたの頭脳をフル回転させて、この知的パズルに挑戦してみませんか?
見どころポイント評価
- 解法の鮮やかさ(風車切り):★★★★★
- もう一つのアプローチ(等積変形):★★★★☆
- 算数の奥深さへの気づき:★★★★★
問題の紹介:一見シンプル、でも奥が深い台形
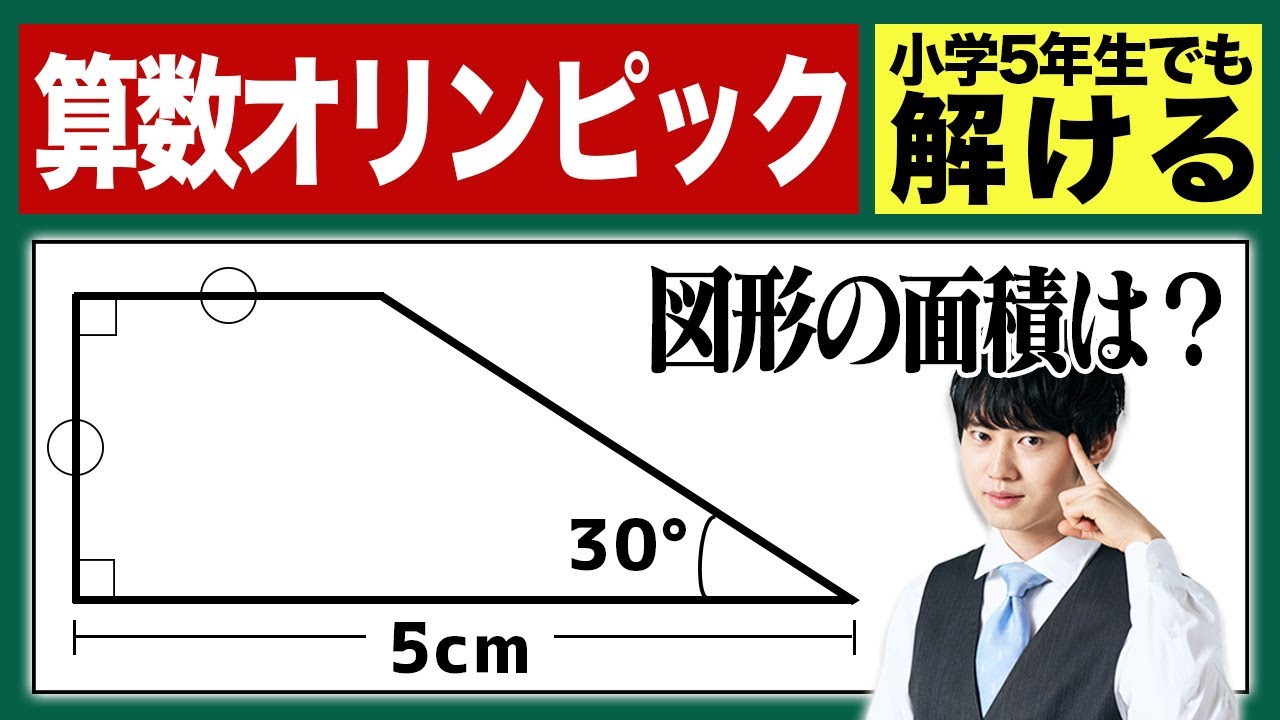
まずは、今回の主役である図形問題を見てみましょう。
問題:下の図のような台形ABCDがあります。AB = AD、∠C = 30°、BC = 5cmのとき、この台形の面積を求めなさい。ただし、平方根(ルート)は使わずに解いてください。
台形の面積を求める公式は「(上底 + 下底)× 高さ ÷ 2」ですよね。しかし、この問題では上底(AD)や高さを直接求めようとすると、どうしてもルートが必要になってしまいます。小学生でも解ける、というところが最大のヒントです。つまり、公式に頼らない別の画期的なアプローチが必要になる、ということですね。一体どんな方法で解くのでしょうか?今回は、驚きの発想で解く2つの方法をご紹介します。
解法1:気分は忍者!?驚きの必殺技「風車切り」
僕がこの問題を初見で解いたときのアプローチが、この「風車切り」です。名前からして、何やらすごそうですよね?
まずは基本に忠実に、図形を分割!
「困難は分割せよ」という言葉があるように、複雑な図形は、まず知っている形に分けて考えるのが定石です。この台形ABCDは、点Dから辺BCに垂線を下ろすと、「正方形」と「直角三角形」の2つに分割できます。
ここで注目すべきは、右側の直角三角形です。∠Cが30°なので、この三角形は角度が30°、60°、90°の、あの三角定規の形をしています。ここまで来ると、「お、何か見えてきたぞ!」と感じる方も多いのではないでしょうか?
必殺技「風車切り」でパズルを組み立てる!
ここからが本番です。この30°、60°、90°の直角三角形を見て、ある有名なテクニックを思い浮かべることができれば、あなたも立派な“算数使い”です。その名も「風車切り」!
この直角三角形を、同じように4つ用意して、風車のように並べてみましょう。すると、どうでしょう!外側に大きな正方形が、そして内側にも小さな正方形が出現するのです。
豆知識:風車切りとは?
風車切りは、特に中学受験の算数でよく使われる図形の考え方です。同じ形の直角三角形を4つ組み合わせることで、面積の関係性や辺の長さを視覚的に捉えやすくする、非常にパワフルなテクニックなんですよ。
そして、ここからがこの解法の最も美しいところです。大きくできた正方形の一辺の長さに注目してください。もとの台形の分割された辺を「丸」と「四角」とすると、大きな正方形の一辺は「丸+四角」で表せます。これって、どこかで見ませんでしたか?そうです、台形の辺BCの長さ「5cm」と全く同じなんです!
つまり、大きい正方形の面積は 5 × 5 = 25 cm2 となります。
最後のピースをはめ込む快感!
さて、私たちが求めたいのは、もとの台形(正方形+直角三角形1つ分)の面積です。風車切りの図全体は、直角三角形4つと内側の小さい正方形でできていますよね。
ここで、30°、60°、90°の三角形の性質を思い出してみましょう。斜辺の長さは、最も短い辺の長さの2倍になります。この関係を使うと、なんと、もとの台形を構成していた「正方形」の部分が、風車切りの内側にできた「小さい正方形」にすっぽりと移動できることがわかるのです!
結果として、私たちが求めたい台形の面積は、大きな正方形をちょうど4つに分けたうちの1つ分と等しくなります。これは見事なパズルだと思いませんか?
したがって、求める面積は、
25 ÷ 4 = 6.25 cm2
と、見事に求めることができました。いやー、気持ちいいですね!
解法2:エレガントで美しい「等積変形」
一つの問題に複数の解法があるのが、算数や数学の醍醐味です。次に紹介するのは、また違った視点からアプローチする、非常にエレガントな解法です。
台形を三角形に変身させる魔法「等積変形」
2つ目のキーワードは「等積変形」です。これはその名の通り、「面積を保ったまま、図形の形を変える」テクニックです。台形のままだと考えにくいので、同じ面積の三角形に変身させてしまいましょう。
具体的には、対角線BDに平行で、頂点Aを通る直線を引きます。そして、辺CDを延長した線との交点をEとします。こうすることで、△ABDと△EBDは、底辺BDが共通で高さが等しいので、面積が同じになります。
これにより、求めたい台形ABCDの面積は、△BCEの面積と等しいということが分かります。これで、問題は「底辺が5cmの△BCEの高さを求める」という、よりシンプルなものになりました!
鍵を握る「30°-75°-75°」の二等辺三角形
ここで、角度に注目してみましょう。もとの図形から、△ABDが直角二等辺三角形であることはすぐに分かります。したがって、∠ABDは45°です。様々な角度を計算していくと、なんと∠EDBが75°になることが分かります。
ここで、算数好きならピンとくるかもしれない、ある特殊な二等辺三角形の性質を使います。それは「頂角が30°、底角が75°の二等辺三角形」です。
豆知識:30°-75°-75°の二等辺三角形の秘密
この三角形は、非常に面白い性質を持っています。2つ組み合わせると、なんと頂角60°の正三角形が内部に現れるのです。この性質から、「底辺の半分の長さが、高さに等しい」という関係が導き出せます。
そして、驚くべきことに、先ほど等積変形で作り出した△EBDが、まさにこの「30°-75°-75°の二等辺三角形」になっているのです!なぜなら、△ABDが直角二等辺三角形であることから、△EBDの高さが底辺BDのちょうど半分になっている、ということが証明できるからです。
この発見が、この問題のクライマックスです!
見事に高さが求まる!
△EBDが30°-75°-75°の二等辺三角形だと分かったことで、私たちが面積を求めたかった△BCEもまた、30°-75°-75°の二等辺三角形であることが確定します。
ということは、先ほどの豆知識で紹介した性質が使えますね!△BCEの高さは、底辺であるBC(5cm)のちょうど半分になります。
高さ = 5 ÷ 2 = 2.5 cm
ここまでくれば、あとは簡単です。三角形の面積公式に当てはめましょう。
面積 = 底辺 × 高さ ÷ 2 = 5 × 2.5 ÷ 2 = 6.25 cm2
見事に、一つ目の解法と同じ答えにたどり着きました!
視点を変えれば世界は変わる!算数の面白さを再発見
いかがでしたでしょうか?今回は、「風車切り」というパズルのような解法と、「等積変形」というエレガントな解法の2つをご紹介しました。どちらの方法も、ルートを使わずに、小学生が持つ知識だけで見事に答えにたどり着けるようになっています。
この問題は、私たちに大切なことを教えてくれます。それは、「一見難しそうな問題も、視点を変えたり、補助線を一本引いたりするだけで、驚くほどシンプルな姿を現すことがある」ということです。公式をただ暗記するだけでなく、図形を柔軟に捉え、その性質を最大限に活用することの面白さを、この問題は体現しています。
普段の仕事や生活で行き詰まったときも、この図形問題のように、少し視点を変えてみることで、思いがけない解決策が見つかるかもしれませんね。ぜひ、頭の体操として、身の回りの方にこの問題を出してみてはいかがでしょうか?



コメント